What Does Quadratic Relationship Mean in Math
A quadratic relationship in math refers to a relationship where one variable is related to the square of another variable. It is a mathematical relationship that can be expressed through a quadratic equation.
When studying mathematical relationships, it is important to understand the concept of a quadratic relationship. In mathematics, a quadratic relationship refers to a relationship between two variables, where one variable is related to the square of another variable. This type of relationship can be expressed through a quadratic equation.
Quadratic relationships are used to model various phenomena, such as projectile motion, parabolic shapes, and economic supply and demand curves. By understanding quadratic relationships, mathematicians and scientists can analyze and predict outcomes in a variety of fields. We will explore the concept of quadratic relationships and their significance in mathematics.
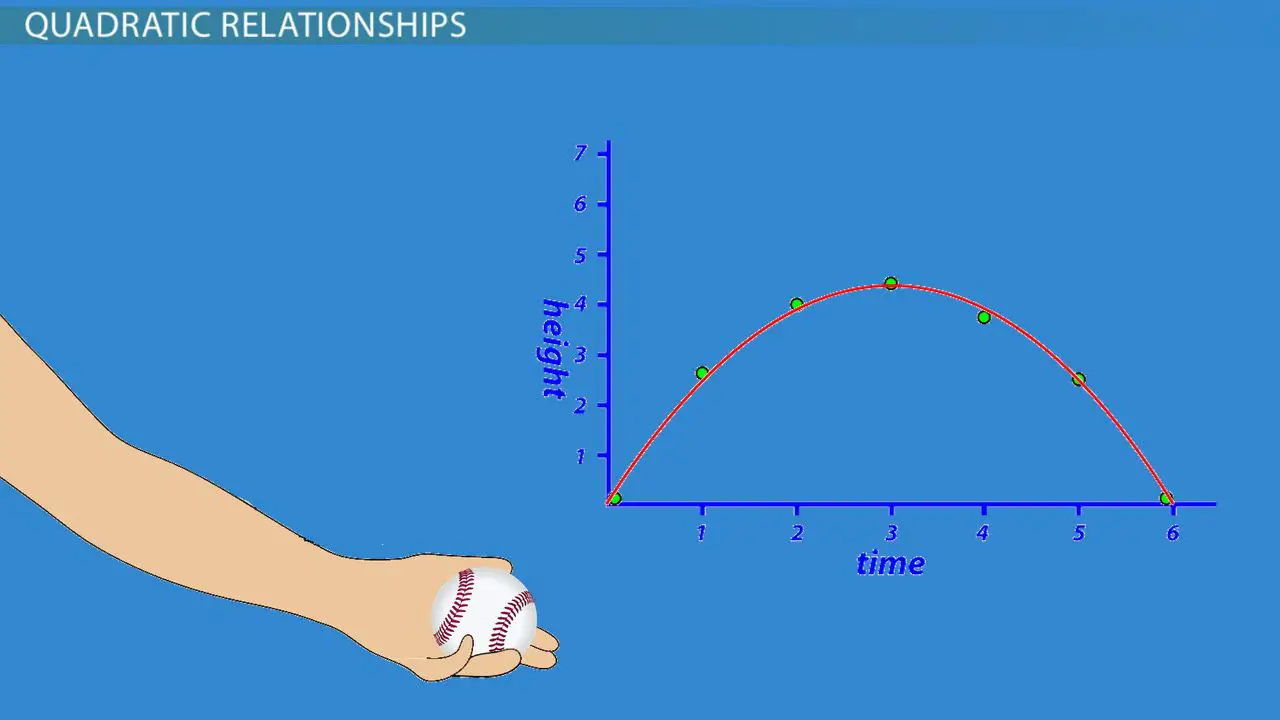
Quadratic Relationship In Math: An Overview
A quadratic relationship is a fundamental concept in mathematics that involves the study of quadratic equations and their properties. Understanding quadratic relationships is crucial for various applications in mathematics and real-life scenarios. In this blog post, we will explore what a quadratic relationship is, why it is important in math, real-life applications of quadratic relationships, and the key components and properties of quadratic equations. Let’s dive in!
What Is A Quadratic Relationship?
A quadratic relationship is a mathematical relationship between two variables, where one variable is a function of the square of the other variable. In simpler terms, it represents a curve on a graph that is shaped like a parabola. Quadratic relationships can be expressed using quadratic equations.
A quadratic equation can be written in the form: ax2 + bx + c = 0, where x represents the variable, and a, b, and c are constants. The highest power of x is 2, hence the term “quadratic.”
Why Are Quadratic Relationships Important In Math?
Quadratic relationships are of great significance in mathematics for several reasons:
- They provide a fundamental understanding of how variables can be related to each other in a non-linear way.
- Quadratic relationships help solve various real-life problems that involve finding the maximum or minimum values.
- They are a key building block for higher-level mathematical concepts like calculus.
Real-life Applications Of Quadratic Relationships
Quadratic relationships are not just theoretical concepts; they have real-life applications in various fields. Some practical examples include:
- Physics: Quadratic relationships are used to analyze the motion of objects under the influence of gravity, such as projectile motion.
- Engineering: Quadratic relationships help in optimizing parameters for designs, such as determining the maximum efficiency of a bridge arch.
- Economics: Quadratic relationships are utilized in analyzing cost and revenue models, determining profit maximization, and understanding market demand.
Understanding The Components Of A Quadratic Equation
To fully comprehend quadratic relationships, it is essential to understand the components of a quadratic equation.
| Component | Description |
|---|---|
| a | The coefficient of the quadratic term. It determines the steepness and direction of the parabola. |
| b | The coefficient of the linear term. It affects the position of the vertex and the line of symmetry. |
| c | The constant term. It determines the y-intercept of the quadratic equation. |
Key Properties Of Quadratic Relationships
Quadratic relationships possess several important properties that help us analyze and solve quadratic equations effectively:
- Vertex: The vertex is the point where the parabola reaches its maximum or minimum value. It is given by the formula x = -b / (2a).
- Axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex, dividing the parabola into two symmetric parts.
- Maximum/minimum value: Depending on the direction of the parabola, it can have a maximum or minimum value at the vertex.
- X-intercepts: These are the points where the graph of the quadratic equation intersects the x-axis.
- Y-intercept: The y-intercept is the point where the graph intersects the y-axis, and its value is given by evaluating the quadratic equation at x = 0.
By understanding these key properties, we can gain insights into the behavior and characteristics of quadratic relationships.
Exploring Quadratic Equations
Quadratic equations play a significant role in mathematics and have various real-world applications. In this section, we will delve into the definition, characteristics, and different forms of quadratic equations. Let’s explore the fascinating world of quadratic equations!
Definition And Characteristics Of Quadratic Equations
Quadratic equations are polynomial equations of degree 2, represented as ax^2 + bx + c = 0, where a, b, and c are constants. The highest exponent in a quadratic equation is always the square of a variable (x^2).
- They form a parabolic curve when graphed.
- The graph of a quadratic equation is symmetric with respect to the line of symmetry.
- Quadratic equations can have zero, one, or two real solutions depending on the discriminant.
- The discriminant determines the nature of the solutions (real, complex, or imaginary).
Differentiating Between Linear And Quadratic Equations
While both linear and quadratic equations involve variables and constants, there are distinct differences between them.
| Linear Equations | Quadratic Equations |
|---|---|
| Have a degree of 1 | Have a degree of 2 |
| Form a straight line when graphed | Form a parabolic curve when graphed |
| Have one solution | Can have zero, one, or two solutions |
| Represented in the form of y = mx + c | Represented in the form of ax^2 + bx + c = 0 |
Forms Of Quadratic Equations: Standard, Vertex, And Factored Form
Quadratic equations can be represented in different forms, each providing unique insights into the equation.
- Standard form: The standard form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants.
- Vertex form: The vertex form of a quadratic equation is given as y = a(x-h)^2 + k, where (h, k) represents the coordinates of the vertex.
- Factored form: The factored form of a quadratic equation is written as a(x-r1)(x-r2) = 0, where r1 and r2 are the roots (or solutions) of the equation.
Example Problems Illustrating Quadratic Equations
To solidify our understanding of quadratic equations, let’s take a look at a few example problems:
Solve the quadratic equation 2x^2 – 5x + 2 = 0.
Find the vertex and axis of symmetry of the quadratic equation y = x^2 + 6x + 8.
Factorize the quadratic equation 3x^2 – 7x – 6 = 0.
By solving these example problems, we can better comprehend the application and importance of quadratic equations in various mathematical contexts.
Graphing Quadratic Relationships
Graphing quadratic relationships is an essential skill in mathematics that allows us to visually represent and interpret the behavior of quadratic equations. By plotting these equations on a graph, we can gain valuable insights into their properties and understand their real-life applications. In this section, we will explore how to graph quadratic relationships and analyze the various elements that contribute to the overall shape and behavior of the graph.
Understanding The Graph Of A Quadratic Equation
Before we delve into the specifics of graphing quadratic relationships, let’s first understand the basic structure of a quadratic equation’s graph. The graph of a quadratic equation, also known as a parabola, takes on a distinctive curved shape. It has a single highest or lowest point called the vertex.
The vertex represents the turning point of the parabola and is vital in determining its behavior. The graph can either open upwards, forming a U-shape, or open downwards, creating an inverted U-shape. The shape and direction of the parabola are affected by the quadratic coefficient (a) in the equation, which determines whether the graph is narrow or wide.
How To Plot The Vertex, Axis Of Symmetry, And X-intercepts
In order to graph a quadratic equation accurately, it is essential to identify and plot key elements such as the vertex, axis of symmetry, and x-intercepts.
- The vertex can be found using the formula: x = -b / (2a). The x-coordinate of the vertex corresponds to the axis of symmetry.
- The axis of symmetry is a vertical line that divides the parabola into two symmetrical halves. The equation of the axis of symmetry can be represented as x = [value of x-coordinate of the vertex].
- The x-intercepts, also called roots or zeros, represent the points where the graph intersects the x-axis. To find the x-intercepts, we set the equation equal to zero and solve for x.
Analyzing The Shape And Direction Of The Parabola
Once we have plotted the vertex, axis of symmetry, and x-intercepts, we can analyze the shape and direction of the parabola.
- If the coefficient of the x^2 term is positive, the parabola opens upwards and has a minimum value at the vertex.
- If the coefficient of the x^2 term is negative, the parabola opens downwards and has a maximum value at the vertex.
Interpreting Real-life Scenarios Based On The Graph Of A Quadratic Equation
Understanding the graph of a quadratic equation allows us to interpret real-life scenarios and make informed decisions. By examining the vertex and shape of the parabola, we can gather valuable insights about various phenomena.
- For example, in physics, the graph of a projectile’s height versus time can be modeled by a quadratic equation. Analyzing the vertex of the parabola provides valuable information about the object’s maximum height and the time it takes to reach it.
- In business, a quadratic equation can help determine the profit-maximizing point for a company by analyzing the vertex and the direction of the parabola.
Graphing quadratic relationships is a valuable tool that enables us to visually represent and understand mathematical and real-world scenarios. By accurately plotting the vertex, axis of symmetry, and x-intercepts, and analyzing the shape and direction of the parabola, we can gain valuable insights and make informed decisions.
Solving Quadratic Equations
Quadratic equations are an essential component of algebra, and understanding how to solve them is crucial for success in math. In this section, we will explore different methods for solving quadratic equations, namely factoring, completing the square, and using the quadratic formula. We will also delve into step-by-step examples to help you grasp the concepts more effectively. Additionally, we will discuss how to identify the number and nature of solutions, including whether they are real, imaginary, or complex.
Methods For Solving Quadratic Equations: Factoring, Completing The Square, And Using The Quadratic Formula
When it comes to solving quadratic equations, there are three main methods: factoring, completing the square, and using the quadratic formula. Each method has its advantages and may be more suitable for certain equations. Let’s take a closer look at each method to better understand their characteristics.
| Method | Characteristics |
|---|---|
| Factoring | Factoring involves breaking down the quadratic equation into its factors. By finding the factors, we can determine the values that satisfy the equation. Factoring is especially useful when dealing with quadratic equations that have simple, factorable expressions. |
| Completing the Square | Completing the square aims to transform the quadratic equation into a perfect square trinomial. This method involves rearranging the equation and adding a constant term to create a square. Completing the square is often used when factoring is not straightforward or the equation lacks rational roots. |
| Using the Quadratic Formula | The quadratic formula is a universal method for solving any quadratic equation. It provides a formulaic approach by substituting the coefficients of the quadratic equation to obtain the values of x. This method is reliable and often preferred when other methods become complex or inapplicable. |
Step-by-step Examples Of Solving Quadratic Equations Using Different Methods
Let’s now explore step-by-step examples of solving quadratic equations using the various methods mentioned. This will help solidify your understanding and provide a practical perspective on applying each method.
Example 1: Solving by Factoring
- Identify the equation: 2x^2 + 7x + 3 = 0
- Factor the quadratic equation: (2x + 1)(x + 3) = 0
- Set each factor equal to zero:
2x + 1 = 0
x + 3 = 0 - Solve for x:
2x = -1, x = -1/2
x = -3 - The solutions to the equation are x = -1/2 and x = -3.
Example 2: Solving by Completing the Square
- Identify the equation: x^2 + 4x + 5 = 0
- Convert the equation to vertex form: x^2 + 4x = -5
- Complete the square by adding and subtracting the square of half the coefficient of x:
x^2 + 4x + (4/2)^2 = -5 + (4/2)^2
x^2 + 4x + 4 = -5 + 4
(x + 2)^2 = -1 - Take the square root of both sides:
x + 2 = ±√(-1) = ±i - Solve for x:
x = -2 ± i - The solutions to the equation are x = -2 + i and x = -2 – i.
Example 3: Solving using the Quadratic Formula
- Identify the equation: 3x^2 – 2x – 1 = 0
- Determine the values of a, b, and c:
a = 3
b = -2
c = -1 - Substitute the values into the quadratic formula:
x = (-b ± √(b^2 – 4ac)) / (2a) - Solve for x:
x = (-(-2) ± √((-2)^2 – 4(3)(-1))) / (2(3)) - Simplify the equation:
x = (2 ± √(4 + 12)) / 6
x = (2 ± √16) / 6
x = (2 ± 4) / 6 - The solutions to the equation are x = 1 and x = -1/3.
Identifying The Number And Nature Of Solutions: Real, Imaginary, Or Complex
By solving quadratic equations, we can determine the number and nature of their solutions. The discriminant, which is the expression within the square root of the quadratic formula, plays a crucial role in this identification. Let’s briefly discuss how to interpret the discriminant:
- If the discriminant is a positive real number, there are two distinct real solutions.
- If the discriminant is zero, there is one real solution (a perfect square trinomial).
- If the discriminant is a negative real number, there are two complex solutions (imaginary numbers).
Through the process of solving quadratic equations, we can unveil the numeric nature of their solutions, whether they are real, imaginary, or complex.
How Does a Proportional Linear Relationship Differ from a Quadratic Relationship in Math?
In math, the “proportional linear relationship definition” is a direct relationship where the ratio of the dependent and independent variables remains constant. In contrast, a quadratic relationship involves a squared term, leading to a curved graph. This difference reflects the varying rate of change in the two types of relationships.
Applications Of Quadratic Relationships
Quadratic relationships are an essential concept in mathematics that find a wide range of applications in various fields. From physics to finance, quadratic equations provide valuable insights into real-life scenarios and help model and optimize complex systems. In this section, we will explore some of the practical applications of quadratic relationships and how they are used to analyze and solve problems in different domains.
Projectile Motion: Analyzing The Flight Path Of Objects
One of the most common applications of quadratic relationships is in the analysis of projectile motion. When an object is launched into the air, it follows a curved flight path governed by the laws of physics. By utilizing quadratic equations, we can accurately predict the object’s trajectory, maximum height, and landing point. This information is crucial in diverse fields such as sports, engineering, and military applications. For example, understanding the trajectory of a golf ball allows players to adjust their swing, while engineers use projectile motion principles to design and optimize the trajectory of a rocket or missile.
Modeling And Optimizing Real-life Scenarios Using Quadratic Equations
Quadratic equations play a vital role in modeling and optimizing real-life scenarios. They provide a mathematical framework for understanding complex relationships and help us find the best solutions. For instance, in economics, quadratic equations can be used to model supply and demand curves, enabling us to analyze the market equilibrium and optimize the production and pricing strategies. In environmental studies, quadratic equations help model population growth and determine the carrying capacity of an ecosystem. By solving these equations, we can make informed decisions and take appropriate measures to ensure sustainable development and resource management.
Quadratic Relationships In Physics, Engineering, And Finance
Quadratic relationships have wide-ranging applications in physics, engineering, and finance. In physics, quadratic equations are used to describe the behavior of vibrating systems, harmonic motion, and energy transformations. In engineering, quadratic relationships are found in structural analysis, fluid dynamics, and control systems. In finance, quadratic equations help us optimize investment portfolios, calculate compound interest, and model risk and return. These applications highlight the significance of quadratic relationships in understanding and solving complex problems in various scientific and practical fields.
Practical Examples Demonstrating The Relevance Of Quadratic Relationships In Various Fields
Let’s consider some practical examples to demonstrate the relevance of quadratic relationships in different fields. One classic example is the calculation of the area of a rectangular garden. By understanding the relationship between the length and width of the garden, we can use quadratic equations to find the dimensions that maximize the garden’s area while using a fixed amount of fencing material. Another example is in the field of optics, where quadratic equations are used to determine the focal length of a lens, optimizing the image quality in cameras and telescopes. These examples exemplify how quadratic relationships offer valuable insights and enable us to solve real-world problems efficiently.
In conclusion, quadratic relationships are not merely abstract concepts in mathematics; they have significant applications in various fields. From analyzing projectile motion to modeling real-life scenarios and solving complex problems in physics, engineering, finance, and other domains, quadratic equations provide the tools for understanding, predicting, and optimizing diverse systems. By harnessing the power of quadratic relationships, we can unlock remarkable insights and achieve practical solutions that contribute to advancements in science, technology, and everyday life.
Conclusion
To summarize, understanding the concept of quadratic relationships is fundamental in the field of mathematics. It allows us to represent and analyze various real-life phenomena and patterns. By recognizing the squared term’s impact on the relationship between two variables, we can comprehend the behavior of parabolas and solve practical problems efficiently.
Remembering the key components of a quadratic relationship, such as the vertex, axis of symmetry, and the shape of the graph, empowers us to make accurate predictions and tackle complex mathematical challenges. Embrace this knowledge, and explore the countless applications quadratic relationships have in our world.